经编机电子横移是通过伺服电机驱动梳栉按照不同的工艺进行横移运动。采用电子横移不但克服了机械式横移机构更换品种周期长、产品单调的缺陷，还能生产花高达到8000横列的大花高产品。驱动梳栉横移的伺服电机有直线型和旋转型，直线型伺服电机在控制精度和响应性等方面都优于旋转型伺服电机，但其价格昂贵，以致各研究机构都致力于研究低成本的旋转伺服电机控制高速经编机梳栉横移。目前，采用位置控制模式控制旋转型伺服电机用于多梳经编机时机器转速可达到850r/min，已能满足多梳拉舍尔经编机的要求。然而，要满足高速经编机梳栉横移的高速度、高精度、高响应和高频率起停的要求还有很大难度。虽然采用速度控制模式控制的经编机梳栉横移已经能够用于高速经编机，但机器速度与德国Karl Mayer推出的旋转伺服电机控制梳栉横移的高速经编机还有差距。

        本文设计了一种基于转矩控制模式的经编机电子横移控制系统，在分析该控制模式的电子横移控制原理的基础上，对电子凸轮和PID算法进行设计，推导出电机选型公式，以提高梳栉的横移精度和梳栉横移的动态响应性。从梳栉横移振动和电机实际速度分析出转矩控制模式的高动态响应性。

 

1 转矩控制模式下的控制系统原理

        1.1 转矩控制模式的提出

        在交流伺服系统中，存在三种控制模式，即位置控制、速度控制和转矩控制模式。三者的区别主要是交流伺服系统中位置环、速度环和电流环的三闭环所属控制不同。

        在位置控制模式中，系统中的位置环、速度环和电流环都由伺服驱动器进行控制运算，这样加大了伺服驱动的运算负担，而同时运动控制卡并未发挥作用，以至于使控制系统的响应性明显下降，不能满足高速经编机的高响应性要求。速度控制模式则是位置环由运动控制卡控制，而速度环和电流环由伺服驱动器控制，这样有利于减小伺服驱动器的运算量，但实验证明，这样还不能满足高速经编机高速的要求。通过研究分析，发现运动控制卡的运算速度和精度远高于伺服驱动器，转矩控制模式中运动控制卡控制位置环和速度环，而伺服驱动器控制电流环，即驱动器为转矩回路，转矩命令由控制卡输入模拟电压（-10V～+10V）进行转矩控制。

        因此，本实验极具创新性地将转矩控制模式应用于高速经编机梳栉横移系统中，推翻了多年来学者认为只有位置控制和速度控制模式能够用于位移领域的观点，同时，更充分的发挥了运动控制卡的快速运算功能。

        1.2 转矩控制模式控制梳栉横移原理

 

 

 

 

 

       

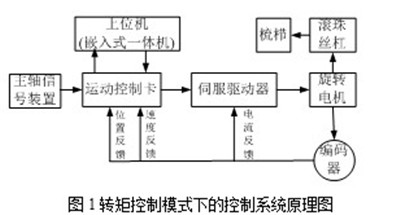
        由图1可知，高速经编机电子横移控制系统在转矩控制模式下，运动控制卡与上位机通讯，接收上位机加载的花型数据，同时通过主轴信号装置采集主轴的当前位置，以确定梳栉横移与静止的时间。运动控制卡在接收到上位机的花型数据与主轴角度信号的同时，旋转电机自带的光电编码器向运动控制卡反馈电机的实际位置和实际速度信号，运动控制卡分析规划的电机运动曲线与实际的电机运动曲线的偏差值，再通过内部PID算法调整参数，以实现偏差量的最小化。运动控制卡完成内部运算后，向伺服驱动器发送电压指令，伺服驱动器通过D/A转换驱动旋转电机的正反运动，滚珠丝杠将电机的旋转运动转化成直线运动，以驱动梳栉进行横移运动。

 

2 电子横移控制系统设计

        2.1 电子凸轮的设计

        在机械式横移机构中，梳栉的横移规律是通过机械凸轮的曲线决定的。在采用转矩控制模式的电子横移系统中，欲实现梳栉的运动与静止的交替状态，就要规划出梳栉的横移运动曲线，亦即电机的位置曲线。本文通过电子凸轮的合理设计，以达到梳栉精确的横移要求。以HKS4经编机为例，其横移角度如表1所示。

 

        

 

 

 

 

 

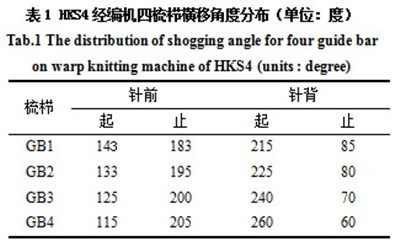
        由表1可知，四把梳栉中GB1的针前横移角度最小，仅为40°，故其要求电机的响应性最高，因此，取GB1为研究对象，以工艺：1-0/2-3//为例。在对电子凸轮进行设计时，针前开始横移时定义为0°，因为针前横移角度为40°，所以在40°时针前横移结束，依此类推完成工艺的一个循环，按照梳栉横移位置要求，设计出电子凸轮曲线，如图2所示。

     

 

 

 

 

 

 

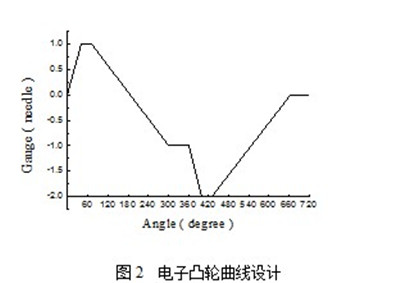
        通过编程手段实现图2所示的曲线，以使电机按照电子凸轮的曲线进行运动。

        2.2 电机选型计算公式设计

        旋转型伺服电机控制的高速经编机电子横移的缺陷是在高速起停运动状态下电机的响应达不到要求，以至于出现滞后现象，进而导致在规定的时间内梳栉不能完成横移运动。在现有技术的条件下，运动控制卡的响应性能远远超过伺服电机的响应性能，因此，选择响应性高的电机是很有必要的，在选择高响应电机的同时，还需考虑负载与电机的惯量比，一般负载惯量比为1～2为最佳匹配，且负载惯量比越接近1，匹配愈佳。

        2.2.1 高响应电机的计算选择

        电机的响应性高的直接表现即伺服电机的加速度大，由公式：a = F/m，要想提高加速度，就需要增加力F，同时减小质量m。同理，如下电机选型计算公式：

                  

       

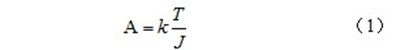
        A：电机的响应参数 T：电机最大转矩（N·m） J：电机转动惯量（10-4 kg·m2） k：系数

        通过研究多种伺服电机的参数规格来选择相对较好的伺服电机，各种规格电机都是选择功率能够达到要求时的最佳参数配比。如表2所示。

      

 

 

 

 

 

 

 

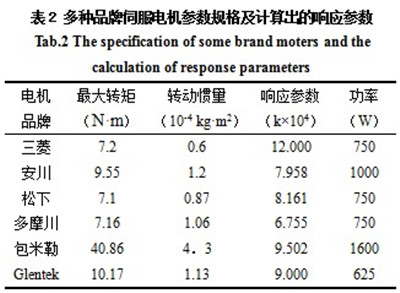
        由表2可明显看出，由电机选型计算公式计算出三菱伺服电机的响应参数远远超过各品牌伺服电机的响应参数。

        2.2.2 负载惯量比的匹配计算

        在选择电机时，惯量匹配也是一个重要的参考因素。本文以HKS4经编机为例，机器宽度为186英寸，机号为28针/英寸。旋转电机控制的梳栉横移的负载包括联轴器、滚珠丝杠和梳栉三部分。

        现将联轴器凹槽部分忽略不计，将其看成均匀圆筒，联轴器转动惯量公式：

        

 

       

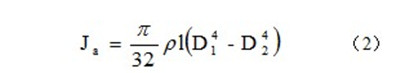
        联轴器密度ρ=2.7×103kg/m3，长度la=55mm，外径D1=42mm，内径D2=16mm。代入数值，可得Ja =4.44×10-5kg·m2。

        滚珠丝杠由两部分组成，在中间螺纹部分较粗，直径D1为20mm，固定丝杠的两端部分较细，直径D2为15mm，计算过程中忽略丝杠上螺纹槽的因素，将其看做均匀圆柱体。滚珠丝杠转动惯量公式：

       

 

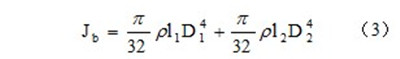
        丝杠材料密度ρ=7.9×103kg/m3，滚珠丝杠总长度lb=205mm，其中l1=135mm，l2=70mm。代入数值，可得Jb=1.95×10-5kg·m2。

        由于梳栉是由滚珠丝杠进行传动，进而进行横移的，因此梳栉等效转动惯量可用下式计算：

                     

 

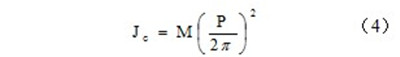
        滚珠丝杠导程P=10mm，负载的质量M=8.5kg。代入数值，可得Jc=2.16×10-5 kg·m2。

        系统负载的总惯量：

                

 

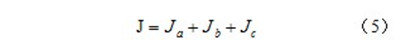
        代入以上计算结果，可得J = 8.55×10-5kg·m2。

        与表2各电机的转动惯量进行对比，可知，与松下电机的负载惯量比为a=0.983＜1，三菱伺服电机负载惯量比为1＜a=1.425＜2；所以可知三菱伺服电机的负载惯量比最佳。

        综合考虑电机的响应性与惯量匹配因素，选择了三菱伺服电机作为转矩控制模式下的高速经编机电子横移的执行机构。

        2.3 PID控制算法设计

        在转矩控制模式下，运动控制卡通过PID控制算法对位置环和速度环进行运算，同时引入速度前馈Kvff和加速度前馈Kaff提高系统的跟随性能。

      

 

 

 

 

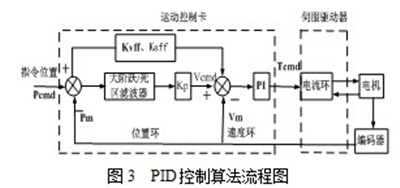
        如图3所示，控制卡接收上位机发下的指令位置，并与编码器反馈回的电机实际位置进行对比，当电机实际位置与理论位置出现偏差△e1时，通过增大位置环比例增益Kp值，能快速使偏差减小直至△e1 = 0，系统的响应速度加快，同时，Kvff和Kaff具有减小系统跟随误差的作用。在位置环中，提供了一个大阶跃/死区滤波器，用于限定每一个采样周期内最大定位误差和进行死区补偿。从位置环输出一个速度指令，控制卡通过编码器反馈的电机速度与指令速度进行对比，得出偏差值△e2，调整速度环比例增益Kvp，积分增益Kvi参数，使△e2 = 0，当增大Kvp值系统出现超调时，增大Kvi值，系统超调量减小，调整直至不出现超调。控制卡完成位置环与速度环的运算后，向伺服驱动器发送一个指令力矩Tcmd，通过电流环，转换成电流指令，控制电机的运动。最终实现了控制信号的调试与发送过程。

        在控制卡内设计了该种PID控制算法过程，既可以提高控制系统的动态响应性，又可以提高系统的定位精度。在伺服驱动内，采用最内环控制，减小伺服驱动的运算负担，使电机的动态响应性大大提高。

 

3 控制系统动态响应测试与分析

        高速经编机电子横移控制系统的研究已经历经数载，经历了位置控制模式向速度控制模式的跨越，通过实验也证明速度控制模式比位置控制模式优越。本文研究的转矩控制模式又是高速经编机电子横移控制系统的一项革新。为了证明转矩控制模式的优越性，本实验通过对梳栉横移振动曲线和梳栉横移定位时间曲线两个角度分析速度控制模式和转矩控制模式下的控制系统的动态响应性。在同样的条件进行实验，实验结果如表3所示。

      

 

 

 

 

 

 

 

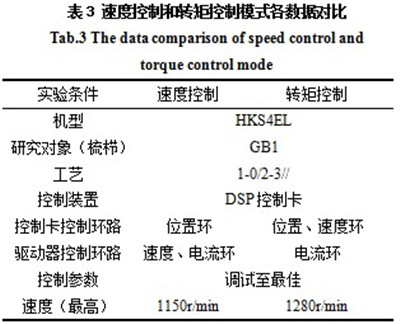
        分别在速度控制模式和转矩控制模式下采用AVD型高精测振仪测量GB1梳栉的加减速所用时间参数，以分析此两种控制模式的动态响应性，各实验参数如表3所示，由于需要在相同的速度下测试，故速度定位1150r/min。测振仪的感应装置安装于推动梳栉横移的滑块上，因此可以忽略梳栉摆动产生的振动对感应装置的影响，只需考虑梳栉横移产生的振动。感应装置能够测出梳栉进行针前和针背横移的振动曲线，如图4、图5所示分别为速度控制模式和转矩控制模式下的梳栉振动曲线图，纵坐标为梳栉横移加速度a（ms2），横坐标为所用时间Time（ms），图中波动较大的曲线段为梳栉在进行针前横移，在水平位置做小范围波动的曲线段为梳栉进行针背横移。由于在机器运行时，针前横移对控制系统的响应性要求最高，所以以下对针前横移曲线段进行研究。

 

 

 

 

 

 

        

 

 

 

 

 

 

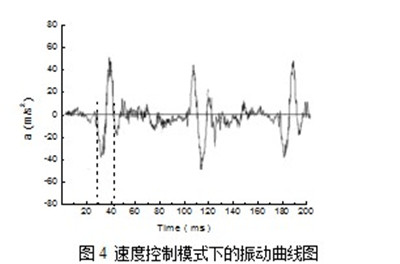
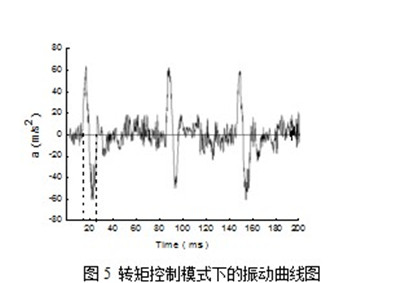
        AVD型高精测振仪测出速度控制模式下梳栉针前横移加减速所用时间为t1=14.1ms。同样，测出转矩控制模式下梳栉针前横移加减速所用时间为t2=11.8ms。

        加减速时间越短，说明控制系统的动态响应性越高，由于t1＞t2，所以，可以分析出转矩控制模式下控制系统的动态响应性高于速度控制模式下控制系统的动态响应性。

        3.2 从电机实际速度分析系统的动态响应性

        伺服电机所带的光电编码器能够反馈电机的实际速度，通过曲线监测软件可以获得电机进行针前针背横移的速度曲线图。图6、图7所示分别为速度控制模式和转矩控制模式下电机的速度曲线图，横坐标为时间Time（ms），纵坐标为电机实际速度V（r/min）。

 

 

 

 

 

 

 

       

 

 

 

 

 

 

 

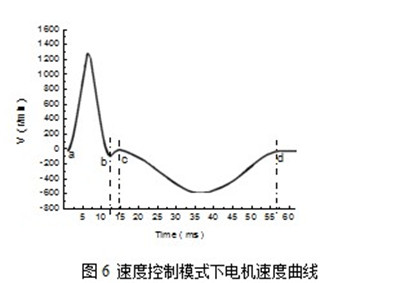
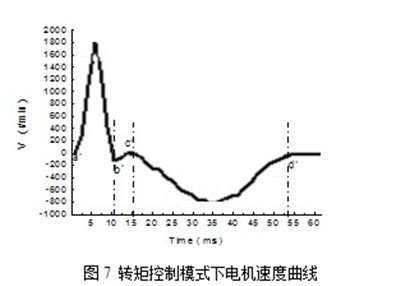
        在图6、图7中，曲线ab段和a′b′段分别为速度控制模式和转矩控制模式下梳栉针前横移时电机的速度曲线，曲线cd段和c′d′段分别为速度控制模式和转矩控制模式下梳栉针背横移时电机的速度曲线。由于梳栉针前横移对电机的动态响应性要求更高，所以对梳栉针前横移进行分析研究。

        在速度控制模式下，速度环是由伺服驱动器进行控制，所以，图6所示曲线是通过伺服驱动器曲线监测软件采集，该曲线显示电机的定位时间为12.4ms，伺服电机的最高转速为1300r/min。在转矩控制模式下，速度环是由PMD控制卡进行控制，所以，图7所示曲线是通过PMD控制卡曲线监测软件采集，该曲线显示电机的定位时间为10.2ms，伺服电机的最高转速为1750r/min。

        从监测软件中分析电机的实际速度曲线，可以明显判断出在转矩控制模式下的经编机梳栉电子横移控制系统的高定位精度和高动态响应性。

 

4 结论

        运用转矩控制模式控制高速经编机梳栉横移已得到成功应用，在成本较低的情况下有效地提高了高速经编机运转过程中梳栉横移的精度，改善了高速经编机的运转性能，经编机生产速度提高了11.3%，布面质量良好。

        （1）在转矩控制模式下，按照梳栉横移的工艺设计出电子凸轮曲线，使梳栉按照电子凸轮进行横移运动，实现梳栉的柔性横移，减少梳栉刚性冲击。

        （2）梳栉横移的实际位置和速度通过PID算法修正，使转矩控制模式下的控制系统具有更高的控制精度。通过在HKS4EL上的对比试验，转矩控制模式在机速提高、电机定位时间、系统高响应性上均优于位置和速度控制模式。

        （3）采用AVD型高精测振仪测出梳栉横移的振动曲线，首次从梳栉横移的振动角度分析控制系统的动态响应性，更进一步证明本文设计的基于转矩控制模式的经编机电子横移的系统的高定位精度和高动态响应性。